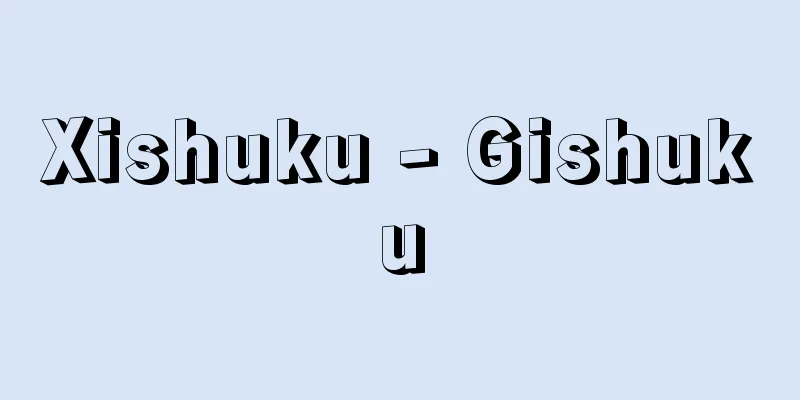One stroke - Hitofudegaki

The question is whether it is possible to draw a figure without ever lifting the pen from the paper or tracing the same lines. This problem has been around for a long time, but in 1736, mathematician Euler published a paper dealing with two themes that are considered to be the precursors of today's topology. One of these themes is the "Königsberg Bridges Problem." This is the question of whether it is possible to cross each of the seven bridges over the Pregel River that runs through Königsberg (now Kaliningrad, Russia) once and return to the original location. Euler proved that in this case, such a route does not exist. In the same paper, he also proved that if the total number of edges (called the local degree) going to and from any vertex in the figure (graph) is even, then the graph can be drawn in one stroke. In the case of Königsberg, the local degrees of each vertex are odd, so it cannot be drawn in one stroke.

Figures (1) to (3) can be drawn in one stroke, but in figures (4) and (5), the local degrees of vertices P and Q are odd, so they cannot be drawn in one stroke. However, if it is not necessary to return to the original point, it is possible to draw the graph in one stroke by starting and ending at points P and Q, respectively. Research is also being conducted on figures (graphs) that can be drawn in two or three strokes.

[Hiroshi Noguchi]

Source: Shogakukan Encyclopedia Nipponica About Encyclopedia Nipponica Information | Legend

筆を紙から一度も離さず、おなじ線をなぞらずに、ある図形が描けるかどうか、という問題。この問題は古くからあったが、1736年に数学者オイラーが、今日のトポロジー（位相幾何学）の先駆とみられる二つのテーマを扱った論文を発表した。その一つのテーマが「ケーニヒスベルクの橋の問題」である。これは、ケーニヒスベルク（現、ロシア領カリーニングラード）を流れるプレーゲル川に架かっている七つの橋を、どれも1回ずつ渡って元の場所に戻ることができるかどうかという問題である。オイラーはこの問題の場合にはそうしたコースは絶対に存在しないことを証明した。また同じ論文で、その図（グラフ）のどの頂点でも、その点に出入りしている辺の総数（局所次数という）がすべて偶数であれば、そのグラフは一筆書きできることを証明した。ケーニヒスベルクの場合、それぞれの頂点の局所次数は奇数であり、一筆書きはできない。

　図の(1)～(3)は一筆書きできるが、図の(4)(5)ではそれぞれ頂点P、Qの局所次数が奇数となり、一筆書きはできない。ただし、元に戻らなくてもよいのであれば、点PかQをそれぞれ書き始め、書き終わりの点にする一筆書きが可能である。二筆書き、三筆書きができる図（グラフ）の研究も行われている。

［野口　廣］

出典　小学館　日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について　情報 | 凡例