Probability - kakuritsu (English spelling) probability

|
The word probability is used in many situations, such as "the probability that it will rain in Tokyo today," "the probability that A-san will be accepted into University B," "the probability that University A will win the league match," and "the probability that a major earthquake will occur in the Tokyo area in the next 10 years." Simply put, probability is a number between 0 and 1 that represents the degree of certainty, with a high degree of certainty being closer to 1 and a low degree of certainty being closer to 0. It can also be expressed as a percentage, such as saying that a probability of 0.3 is 30%. In the cases of the examples given at the beginning, it is not easy to determine a specific and accurate number for the probability, nor is it particularly meaningful. In these cases, a number less than 5%, approximately 50%, or 90% would be sufficient. So, how do we determine the probability that a certain event that occurs by chance will actually occur? When an experiment can be repeated under the same conditions, it is possible to determine the probability as the limit (when the number of repetitions is large) of the relative frequency (when the number of times that an event actually occurred out of N repetitions is n, n/N is called the relative frequency). However, in reality, the number of repetitions is finite, so in reality, only an approximate value can be determined. There are also cases where a constant value can be expected for probability without repeating the experiment. For example, the probability of getting heads when flipping a coin is 1/2, and the probability of getting a six when flipping a dice is 1/6. [Shigeru Furuya] Equally certainWhen a dice is thrown, each number is considered to be equally likely. Laplace defined probability based on the a priori judgment of "equally likely." In other words, in an experiment or observation where the outcome is governed by chance, there are a total of n possible outcomes, and which of these is "equally likely" to occur. In this case, if the number of possible outcomes of the event A in question is a out of n, then the probability of A occurring is defined as a/n. For example, the probability of getting a 6 when throwing a dice is 1/6, and the probability of getting an even number is 3/6, or 1/2. Probabilities can take on different values depending on what you consider to be "equally likely." Here's an example: Suppose you go from A to B via the route shown in without making any detours. Let's find the probability of passing C. [Solution (1)] The way to go from A to B without taking a detour is to take 4 and then 2, i.e., 4 C 2 = 6 ways. On the other hand, there are 2 x 2 = 4 ways to go through C, so the probability we are looking for is 4 out of 6, or 4/6 = 2/3. [Solution (2)] When going from A to B, choose one of two paths with equal probability for the four points A, D, C, and E. In this case, the probability of taking the path from D to C is (1/2) × (1/2) = 1/4, and the probability of taking the path from E to C is also 1/4, so the probability of taking C is 1/4 + 1/4 = 1/2. Which of these two answers is correct? Solution (1) is correct if choosing any of the six paths from A to B is "equally likely." Also, if the choice of which direction to go at each of points A, D, C, and E is "equally likely," then solution (2) is correct. If we interpret this problem literally, solution (2) seems a more natural way of thinking than solution (1). In probability problems related to the number of cases, it is important to clarify what is "equally likely." When considering such probability problems, it is important to break down the cases into "equally likely" cases. When a friend asked Galileo, "When three dice are rolled at the same time, the number of cases in which the sum of the dice is 9 should be the same as the number of cases in which the sum of the dice is 10, so why is it that the sum of the dice is actually more likely to be 10?" Galileo noted that there are 6, 3, and 1 possible cases for (1,2,6), (1,4,4), and (3,3,3), respectively, and answered that there are 6+6+3+3+6+1=25 possible cases for the sum of the dice to be 9 out of 6×6×6=216 possible cases, and 6+6+3+6+3+3=27 possible cases for the sum of the dice to be 10, so the sum of the dice is more likely to be 10. In this way, Galileo was able to obtain the correct result by breaking down the cases into "equally likely" cases. [Shigeru Furuya] History of Probability TheoryThe beginning of probability theory is said to be the several topics that were discussed in the correspondence between Pascal and Fermat in the mid-17th century, but Galileo had been thinking about probability problems even before that. Essentially, what interested Pascal and Fermat was the problem of determining the number of cases. Huygens' "On the Theory of the Game of Dice", published in 1657, consists of 14 propositions, including a probabilistic consideration of dice. Bernoulli generalized Huygens' research results in his posthumously published " Ars Conjectandi " (1713), systematizing the theory of permutations and combinatorial combinations, and formulating the law of large numbers for the first time and providing a proof of it. Since then, many mathematicians have discussed probability, but Laplace completed his "Analytical Theory of Probability" in 1812. This work was a compilation of previous knowledge of probability, using the rapidly developing analysis at the time as a weapon and introducing new methods. Laplace's work became the starting point for subsequent research, and the idea of probability came to be effectively applied in many fields. Probability has become indispensable in statistics in particular. Probability theory up to the 19th century is sometimes called classical probability theory. In the 20th century, probability theory made a great leap forward. Borel showed that when real numbers in the interval (0,1) are expanded into binary, the relative frequency of 1 appearing in the first n places for almost all real numbers (i.e., excluding real numbers belonging to the set of measure 0) approaches 1/2 as n → ∞. Lebesgue also created a general measure theory that includes both Jordan's measure theory and Borel's measure theory as special cases. This measure theory also had a great influence on probability theory, and in 1933 Kolmogorov presented a system of axioms for probability theory based on Lebesgue measures, which established probability theory as a form of mathematics. This is also called measure-theoretic probability theory. This measure-theoretic method is effective for problems that classical probability theory could not address (such as problems with stochastic processes), and is still developing rapidly. The axioms of the basic part of measure-theoretic probability theory are written in terms of sets and measures. In order to enable readers who are not familiar with measure theory to understand the gist of the content, we first explain the axiomatic ideas about probability in a simple case. [Shigeru Furuya] Axiomatic Method of Probability TheoryLaplace defined probability based on the concept of "equally likely". This is sufficient for problems related to the number of cases, such as cards and dice. However, as the range of probability applications expands, there are cases where it becomes impossible to judge "equally likely". Therefore, probability based on relative frequency has also been considered. Mises's theory of probability is representative of this direction. There are various ways of thinking about the meaning of probability itself. However, no matter what meaning is given to it, there should be common basic properties that probability should have. Moving away from questions such as what probability is, we extract the basic properties of probability and construct a theory of probability based on only those, that is, based on a system of axioms. Here, we consider the case where the number of possible cases for a certain random event is finite. A trial is an experiment or observation whose outcome is governed by chance. For example, throwing a dice is a trial. If we denote all possible outcomes in a trial by ω 1 , ω 2 , …, ω n , then the set Ω={ω 1 , ω 2 , …, ω n } An element of the sample space Ω is called an elementary event, and a subset of Ω is called an event. When event A occurs, it means that ω (an element of Ω), which represents the result of a trial, is an element of A. For two events A and B, A∪B and A∩B are called the sum event and product event of A and B, respectively. Ā=Ω-A is called the complement event of A, Ω is all events, and ∅ (= the empty set) is called the empty event. When A∩B=∅, two events A and B are called mutually exclusive events. This means that A and B cannot occur together. For example, suppose there are two winning tickets among five lottery tickets. Consider the following problem regarding a trial in which A draws the lottery ticket first, and then B draws the ticket. 1. Create a sample space for this trial. 2. What subset of this sample space is the event that A hits? 3. What subset of this sample space is the event that B hits? To solve this problem, represent the five lottery tickets as 1, 2, 3, 4, and 5, with 1 and 2 being the winning tickets. If the tickets drawn by A and B are represented as a and b respectively, the result of the trial can be expressed as (a, b) (a ≠ b). Therefore, the sample space consists of 20 elements as shown in Next, the event that A wins consists of the eight elements in the top two rows of the figure. Also, the event that B wins consists of the eight elements in the left two columns. If a function P whose domain is the whole subset of Ω is In the previous lottery example, the underlying events are considered to be "equally likely," so the probability that A, who draws the lottery first, wins and the probability that B, who draws the lottery second, win are both the same value, 2/5. When there are r winning tickets out of n, drawn in exactly the same way, it can be shown that the person who draws the lottery first and the person who draws the lottery second have the same probability of winning. [Shigeru Furuya] Measure-theoretic probability theoryProbability Space, Events, Probability A nonempty set Ω is given. There is a family of sets whose elements are subsets of Ω (called a family of sets because it is a set whose elements are sets), and the following three conditions are satisfied: Given a set Ω and a perfect additive family in Ω, a real-valued function P defined on An element of a set family is called an event, and P(A) is called the probability of event A. ∅ (the empty set) is called the empty event, and Ω is called all events. For events A and B, A∪B and A∩B are called the union event and product event, respectively. For event A, Ā=Ω-A is called the complement of A. When A∩B=∅ for two events A and B, A and B are said to be mutually exclusive events. [Shigeru Furuya] Independence of Events Two events A and B are independent if P(A∩B)=P(A)P(B). [Shigeru Furuya] Random variables, distribution functionsConsider a probability space (Ω,,P). For a real-valued function X defined in Ω, if {ω|X(ω)<a}∈ holds for any real number a, then X is called a random variable. Let Ω be the set R of all real numbers, and let 1 be the set of Borel sets in R. For a random variable X, Φ(A)=P(ω|X(ω)∈A) (A∈ 1 ) For n random variables X 1 , X 2 , …, X n , a vector X=(X 1 ,……,X n ) with X i as its ith component is called an n-dimensional random variable. In this case, the function of n variables F(a 1 ,a 2 ,……,a n )=P(ω|X 1 (ω)≦a 1 , [Shigeru Furuya] Independence of random variables Given a finite number of random variables X 1 , X 2 , …, X n , for any one-dimensional Borel set A i (1≦i≦n), P(ω|X 1 (ω)∈A 1 , …, X n (ω)∈A n ) [Shigeru Furuya] Mean, variance, and standard deviation of random variables For a random variable X, the Lebesgue integral with the above measure P can be considered. If X is integrable with respect to P, then E(aX + bY) = aE(X) + bE(Y) Covariance and correlation coefficient For two random variables X and Y, C(X,Y)=E((X-E(X))(Y-E(Y)))
|ρ(X,Y)|≦1 [Shigeru Furuya] "Foundations of Probability Theory, by Kiyoshi Ito (1944, Iwanami Shoten)" ▽ "Modern Mathematics 14: Probability Theory, by Kiyoshi Ito (1953, Iwanami Shoten)" ▽ "Probability Theory, by Takayoshi Kawata (1948, Kyoritsu Shuppan)" ▽ "Probability Theory and Its Applications, Vol. I, Vol. II, Vol. II, Vol. I, Vol. II, by W. Feller, supervised translation by Tatsuo Kawata and Kiyonori Kunisawa (1960-1970, Kinokuniya Shoten)" [Reference] | | |©Shogakukan "> Probability (equally likely) (Figure A) ©Shogakukan "> Probability (Probability theory by the axiomatic method) [Figure B] Source: Shogakukan Encyclopedia Nipponica About Encyclopedia Nipponica Information | Legend |
|
「今日、東京で雨が降る確率」「A君がB大学に合格する確率」「A大学がリーグ戦で優勝する確率」「今後10年のうちに東京地区で大地震が起こる確率」というように、確率ということばはいろいろな場面で使われている。簡単にいえば、確率は確からしさの程度を0と1との間の数値として表したもので、確からしさの程度が高いとき1に近く、低いとき0に近い。また確率が0.3であることを確率は30%というように、パーセンテージで表すこともある。始めにあげたいくつかの例の場合に、その確率として一つの数値を具体的に正確に定めるのは容易なことではないし、またそれほど意味のあることでもない。これらの例の場合には5%未満とか、ほぼ50%とか90%とかの程度で十分であろう。 さて、偶然的に起こるある事柄が実際に起こる確率をどのように定めるか? 同一条件のもとで繰り返して実験ができる場合には、相対度数(N回の繰り返しのうち実際に起こった回数がnであったときn/Nを相対度数という)の値の極限(繰り返しの回数を大きくしたときの)として確率を定めることができる。ただし実際には繰り返しの回数は有限であるから、具体的には近似的な値が定まるだけである。実験を繰り返し行わなくても確率が一定値をとることが期待される場合もある。たとえば、コインを投げたとき表の出る確率は1/2、さいころを投げたとき6の目の出る確率は1/6などである。 [古屋 茂] 同様に確からしいことさいころを投げたとき、どの目が出るのも同じ確からしさをもつと考えられる。ラプラスは「同様に確からしい」という先験的判断に基づいて確率を定義した。すなわち、結果が偶然に支配されるような実験や観察において起こりうる結果が全部でn通りあり、これらのうちのどれが起こるかが「同様に確からしい」ものとする。このとき着目する事柄Aが起こるのがn通りのうちのa通りであるとすると、Aの起こる確率をa/nと定める。たとえば、さいころを投げたとき6の目の出る確率は1/6であり、偶数の目が出る確率は3/6すなわち1/2である。 何を「同様に確からしい」と考えるかによって確率が別々な値をとることがある。その例をあげよう。 のような道を通って、AからBまで回り道をしないで行くとする。Cを通る確率を求めてみる。 〔解(1)〕AからBへ回り道をしないで行く方法は、4から2をとる組合せ、すなわち4C2=6通りある。一方、Cを通る方法は2×2=4通りあるから、6通りのうちの4通り、すなわち4/6=2/3が求める確率である。 〔解(2)〕AからBへ向かうとき、A、D、C、Eの4点ではどちらへ進むか二つのうちの一つを同じ確からしさで選ぶことにする。このときDからCへの道を通る確率は(1/2)×(1/2)=1/4であり、同じくEからCへの道を通る確率も1/4であるから、Cを通る確率は1/4+1/4=1/2となる。 この二つの解答のどちらが正しいか。AからBへの6通りの道のどれを選ぶかが「同様に確からしい」ときは解(1)が正しい。またA、D、C、Eの各点でどちらへ進むかその選び方が「同様に確からしい」ときは解(2)が正しい。この問題をことばどおりに解釈すると、解(2)のほうが解(1)よりも自然な考え方のように思われる。 場合の数に関連する確率の問題では、何が「同様に確からしい」かを明確にすることが重要であって、このような確率の問題を考えるとき、「同様に確からしい」場合にまで場合を分解して考えることがたいせつである。「三つのさいころを同時に投げると、目の和が9になる場合の数と、目の和が10になる場合の数とは同じはずであるのに、実際は和が10になるほうが起こりやすいのはなぜか」と友人に尋ねられたガリレイは、(1,2,6)、(1,4,4)、(3,3,3)の起こり方はそれぞれ6通り、3通り、1通りであることに注目し、目の和が9になるのは6×6×6=216通りのうちの6+6+3+3+6+1=25通り、目の和が10になるのは6+6+3+6+3+3=27通りであるので、和が10になるほうが起こりやすいと解答を与えたという。このようにガリレイは「同様に確からしい」場合にまで分解して考えたから正しい結果が得られたのである。 [古屋 茂] 確率論の歴史17世紀のなかばごろにおけるパスカルとフェルマーの文通で取り上げられたいくつかの話題が確率論の始まりといわれているが、それ以前にもガリレイが確率の問題を考えている。パスカル、フェルマーが興味をもったのは、本質的には場合の数を求める問題であった。1657年に出版されたホイヘンスの『さいころ遊びの理論について』は、14の命題からなっているが、そのなかには、さいころについて確率論的に考察したものが含まれている。ベルヌーイはその死後刊行された『推論法』Ars Conjectandi(1713)において、ホイヘンスの研究結果を一般化し、順列・組合せ理論を系統づけ、また初めて大数(たいすう)の法則を定式化してその証明を与えている。以後多くの数学者が確率について論ずるようになったが、ラプラスは1812年に『確率の解析的理論』を完成した。これは、当時、目覚ましい発展を続けていた解析学を武器とし、新しい手法を導入して、それまでの確率の知識を集大成したものである。このラプラスの業績は以後の研究の出発点ともなり、確率の考えは多くの分野で効果的に応用されるようになった。とくに統計学においては確率は欠くことのできないものとなった。19世紀までの確率論を古典確率論とよぶこともある。 20世紀になって確率論は大きく飛躍した。ボレルは、区間(0,1)の実数を二進展開したとき、ほとんどすべての実数に対して(すなわち測度0の集合に属する実数を除いて)n位までに現れる1の相対度数がn→∞のとき1/2に近づくことを示した。またルベーグは、ジョルダンによる測度論およびボレルによる測度論の両方を特別の場合として含むような一般的な測度論をつくりあげた。この測度の理論は確率論にも大きな影響を与え、1933年にコルモゴロフは、ルベーグ式測度に基づく確率論の公理系を提示して数学としての確率論が確立された。これは測度論的確率論ともよばれている。この測度論的方法は、古典的確率論では手がつけられなかった問題(たとえば確率過程の問題など)に対しても有力であって、現在も急速に発展しつつある。測度論的確率論の基本的部分の公理系は集合と測度のことばを使って書かれている。測度理論に詳しくない読者にもその内容の大筋だけは理解できるように、次にまず、確率についての公理的考えを簡単な場合について説明しておく。 [古屋 茂] 公理的方法による確率論ラプラスは「同様に確からしい」という概念を基にして確率を定義した。カードやさいころなど、場合の数に関連する問題に対してはこれで十分であろう。しかし、確率が応用される範囲が拡大されてくると、「同様に確からしい」という判断が不可能になる場合も生じる。そこで相対度数を基にした確率も考えられるようになった。この方向を代表するものはミーゼスの確率論である。確率の意味そのものについてはいろいろな考え方がある。しかしどのような意味づけをしようとも、確率としてもつべき共通の基本的性質があるはずである。確率とは何かというような問題から離れて、確率のもつ基本的な性質を抜き出し、それだけを基にして、すなわち公理系を基にして確率論を構成するのである。ここでは、ある偶然的な事柄で起こりうる場合の数が有限個である場合を考える。 結果が偶然に支配されるような実験または観測を試行ということにする。たとえば、さいころを投げるのは一つの試行である。ある試行において起こりうる結果の全体をω1、ω2、……、ωnで表すとき、集合 標本空間Ωの元を根元事象といい、Ωの部分集合を事象という。事象Aが起こるというのは、試行の結果を表すω(Ωの元)がAの元であることを意味する。二つの事象A、Bに対してA∪B、A∩BをそれぞれA、Bの和事象、積事象という。Ā=Ω-AをAの余事象、Ωを全事象、∅(=空集合)を空事象という。 A∩B=∅のとき、二つの事象A、Bを排反事象という。これはAとBがともに起こることがないことを表している。たとえば、5本のくじのうちに2本の当たりくじがあるとする。このくじをまずAが、次にBが引くという試行について次のような問題を考える。 ①この試行の標本空間をつくれ。②Aが当たるという事象はこの標本空間のどんな部分集合か。③Bが当たるという事象はこの標本空間のどんな部分集合か。 これを解くために5本のくじを1、2、3、4、5で表し、1と2が当たりくじとする。A、Bが引いたくじをそれぞれa、bで表せば、試行の結果は(a,b)(a≠b)で表される。したがって標本空間はのような20個の元よりなる。次にAが当たるという事象は図で上の2行の8個の元よりなる。またBが当たるという事象は左の2列の8個の元よりなる。 Ωの部分集合全体を定義域とする関数Pが 前のくじの例では、根元事象は「同様に確からしい」と考えられるから、初めにくじを引くAが当たる確率も、次に引くBが当たる確率も同じ値の2/5となる。まったく同じ方法でn本のうちr本の当たりくじがあるとき、初めにくじを引く人も、次に引く人も、当たる確率は同じであることが示される。 [古屋 茂] 測度論的確率論確率空間、事象、確率空集合でない集合Ωが与えられている。Ωの部分集合を元とするある集合族(は集合を元とする集合であるから集合族とよぶ)があって、次の三つの条件 集合ΩとΩにおける完全加法族が与えられたとき、で定義された実数値関数Pが次の条件 集合族の元を事象といい、P(A)を事象Aの確率という。∅(空集合)を空事象、Ωを全事象という。事象A、Bに対してA∪B、A∩Bをそれぞれ和事象、積事象とよぶ。事象Aに対してĀ=Ω-AをAの余事象という。二つの事象A、Bに対してA∩B=∅のときA、Bは排反事象であるという。 [古屋 茂] 事象の独立二つの事象A、Bが独立であるとは [古屋 茂] 確率変数、分布関数確率空間(Ω,,P)を考える。Ωで定義された実数値関数Xについて、任意の実数aに対して{ω|X(ω)<a}∈が成り立つとき、Xを確率変数という。Ωを実数全体の集合Rとし、1をRにおけるボレル集合の全体とする。 確率変数Xに対して n個の確率変数X1、X2、……、Xnに対してXiを第i成分とするベクトルX=(X1,……,Xn)をn次元確率変数という。このとき、n変数の関数 [古屋 茂] 確率変数の独立性有限個の確率変数X1、X2、……、Xnが与えられたとき、任意の一次元ボレル集合Ai(1≦i≦n)に対して [古屋 茂] 確率変数の平均値、分散、標準偏差確率変数Xに対して、上の測度Pによるルベーグ積分が考えられXがPに関して積分可能であれば E(aX+bY)=aE(X)+bE(Y) 共分散と相関係数二つの確率変数X、Yに対して
|ρ(X,Y)|≦1 [古屋 茂] 『伊藤清著『確率論の基礎』(1944・岩波書店)』▽『伊藤清著『現代数学14 確率論』(1953・岩波書店)』▽『河田敬義著『確率論』(1948・共立出版)』▽『W・フェラー著、河田竜夫・国沢清典監訳『確率論とその応用 Ⅰ上下 Ⅱ上下』(1960~1970・紀伊國屋書店)』 [参照項目] | | |©Shogakukan"> 確率(同様に確からしいこと)〔図A〕 ©Shogakukan"> 確率(公理的方法による確率論)〔図B〕 出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例 |
Recommend
time
...Time is something that is maintained in all ch...
Aizen-ko
〘Noun〙① Buddhist term. A Buddhist ceremony held to...
Carthamin
C 43 H 42 O 22 (910.77). The petals of Carthamus ...
Provisional payment - Karinoufu
...All of these effects arise according to the co...
Engel Method
...The former is also called the market basket me...
Motoarakawa - Motoarakawa
A river that flows southeast through eastern Saita...
Shudra - Shudra (English spelling) Śūdra
One of the four social classes (varnas) that exis...
Echizen ware
Pottery made in the Nyu District area of Fukui ...
Taihaku
[1][一] Abbreviation of "Taihakusei (Taihaku S...
Schulz, CM (English spelling) SchulzCM
…A beagle dog that appears in the newspaper comic...
Senka paper - Senka paper
Also written as senka-shi. (1) Originally, it refe...
Phosphoric acid (phosphoric acid)
The acids formed by the hydration of diphosphorus ...
Helmuth Plessner
1892‐1985 German philosopher. Born in Wiesbaden. S...
Condensation
Also called condensation. When gas is cooled below...
Macao - Macao (English spelling)
A former Portuguese colony on the west bank of th...
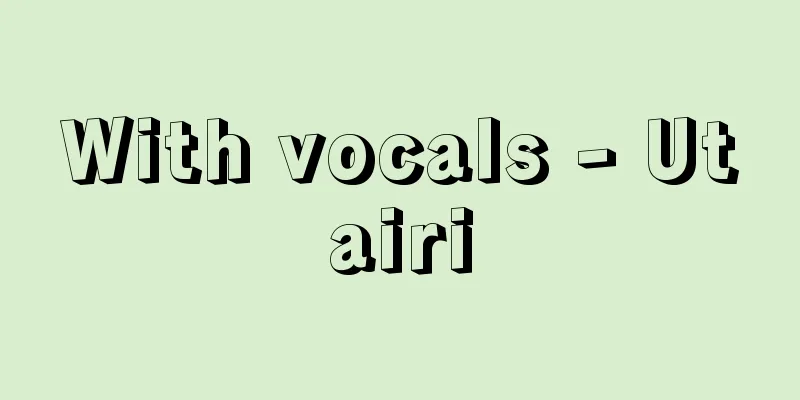




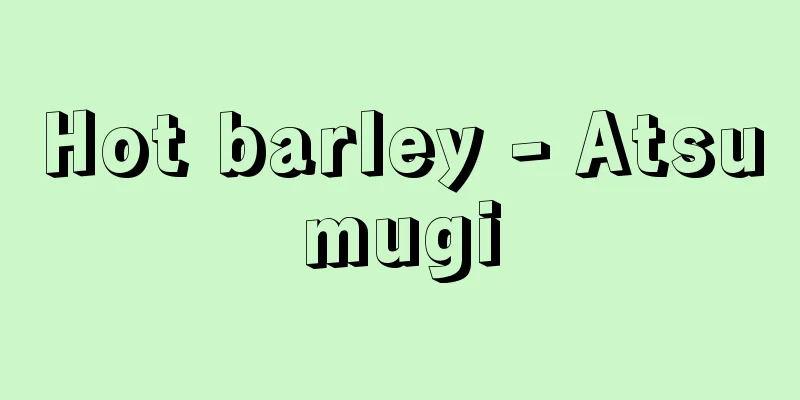


![Kish [island] - Kish](/upload/images/67d0480af2d55.webp)