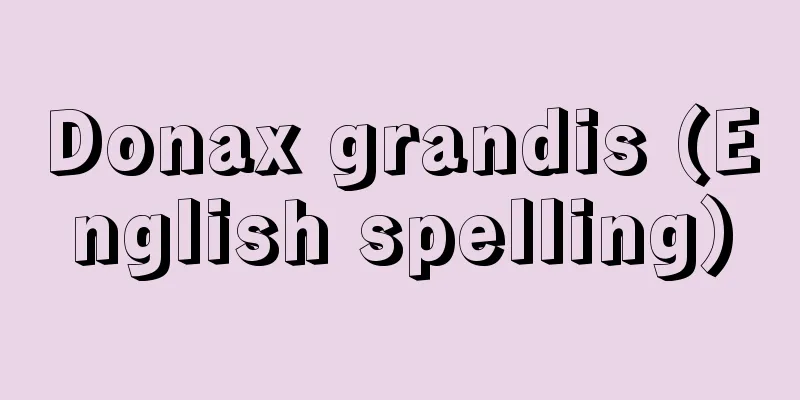Continued fraction

|
Of the fractions The approximate fraction P n /Q n of a regular continued fraction is P n+1 =P n a n +P n-1 , [Tsuneo Adachi] Source: Shogakukan Encyclopedia Nipponica About Encyclopedia Nipponica Information | Legend |
|
分数のうち 正則連分数の近似分数Pn/Qnは [足立恒雄] 出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例 |
>>: Rembrandt - Rembrandt van Rijn
Recommend
Ako King - Akoou
…She is a prostitute from Shimizuzaka who appears...
Documents in the womb - Tainai Monjo
Documents placed inside statues of Buddha and deit...
Canalo
Argentine tango band leader and composer. He taugh...
Homespun - Homespun (English spelling)
Originally, it was a woolen fabric made using thi...
Tadmor
…The ruins are located about 200 km northeast of ...
Shinzo Ueki
…In the Muromachi period, Sarugaku Noh performanc...
Imprimatura - Imprimatura
…In the second half of the 15th century, oil pain...
Orthoceratida
…the genus that represents the Orthoceradinida or...
First term - Ichigobun
〘noun〙 A form of property inheritance in the Middl...
Qiu Jin - Qiu Jin
A Chinese revolutionary in the late Qing Dynasty....
svara
…There is no soaring into the air or moving aroun...
Ichiden Sanshu - Ichiden Sanshu
...This fact shows that the cultivation rights es...
Kazama Jokichi
1902-1968 A social activist in the Showa era. Bor...
《Aktion》 - Aktion
...Schoenberg's tragic pathos, which called f...
Pietra dura (English spelling) [Italy]
The term refers to hard stones, such as gemstones,...

![Ariake [town] - Ariake](/upload/images/67cadc3662d09.webp)