Sequence - Suuretsu

|
A sequence of numbers a 1 , a 2 , a 3 , a 4 , … arranged in correspondence with each of the natural numbers 1 , 2 , 3 , 4 , … is called a sequence. Each of these numbers is called a term of the sequence, and from the beginning, they are called the first term, the second term, the third term, …. When the nth term of a sequence is considered to be representative of each term, it is called the general term. The general term is often given as an expression for n . There are finite sequences, which end with a finite number of terms, and infinite sequences, which continue indefinitely. The last term of a finite sequence is called the terminal term. Arithmetic sequences and geometric sequences are often used as examples of sequences. However, there are many other types of sequences as well. Given a sequence of numbers a 1 , a 2 , …, the sum of the first to nth terms is often a problem. This is called a n = f ( a 1 , a 2 ,……, a n -1 ) a 1 = 1, a 2 = 1, a n = a n -1 + a n -2 The limit of an infinite sequence is a discussion of what happens as we go further into it. Sometimes we investigate what happens when we add to an infinite sequence starting from the first term. A sequence a 1 + a 2 + ……, which is formally connected by a plus sign to form a series , is called a series. [Osamu Takenouchi] [Reference items] | | | | |©Shogakukan "> Sums of commonly used sequences Source: Shogakukan Encyclopedia Nipponica About Encyclopedia Nipponica Information | Legend |
|
自然数1, 2, 3, 4,……のおのおのに対応して並べられた数の列a1, a2, a3, a4,……を数列という。そのおのおのの数を数列の項といい、初めから順に、初項、第2項、第3項、……という。数列の第n項をおのおのの項の代表と考えるとき、これを一般項という。一般項は、nの式として与えられることが多い。数列には、項が有限個で終わる有限数列と、どこまでも続く無限数列とがある。有限数列の最後の項を末項という。数列の例としては等差数列、等比数列などがよく扱われる。しかし、そのほかにも、いろいろな数列がある。 数列a1, a2,……が与えられたとき初項から第n項までの和がよく問題になる。これを記号 an=f(a1, a2,……, an-1) a1=1, a2=1, an=an-1+an-2 無限数列が、先のほうにいくとどうなるかを論ずるのが数列の極限の議論である。無限数列を初項から順に加えていくとどうなるかを調べることがある。数列a1, a2,……を形式的にプラス記号で結んだa1+a2+……を級数という。 [竹之内脩] [参照項目] | | | | |©Shogakukan"> よく使われる数列の和 出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例 |
>>: Quantitative economic history
Recommend
Glass wool
…Made of molten glass in a filament, it is also c...
Wang Xiu Lu - Wang Xiu Lu
…A leading figure in the cultural and publishing ...
Abhinaya - Abhinaya
…From the 11th to 12th centuries, many of the dan...
Mansfield, Sir Peter
Born: October 9, 1933, London [Died]2017.2.8. Brit...
Ishige Tsumugi
…The central settlement of Ishige flourished in t...
Bag lining - Fukuroji
Land surrounded by other people's land and wi...
Trautwein, F. (English spelling) TrautweinF
...Various timbres are created by using a sound s...
Ishikari Nabe - Ishikari Nabe
…In recent years, due to the concentration of pop...
Equilibrium exchange rate
…G. Cassel’s theory that under a freely floating ...
Greek science
A general term for the sciences promoted and devel...
Drongo (Drongo) - Drongo (English spelling)
A general term for birds in the passerine family D...
synthesis
...(3) Keto acid lyases, which carry out condensa...
Japanese palolo (English spelling) Japanesepalolo
…Such reproductive individuals are called bachi, ...
School Kendo
...The unification of styles, which was essential...
Windward Islands - Kazakami
...Many of the islands are volcanic and surrounde...

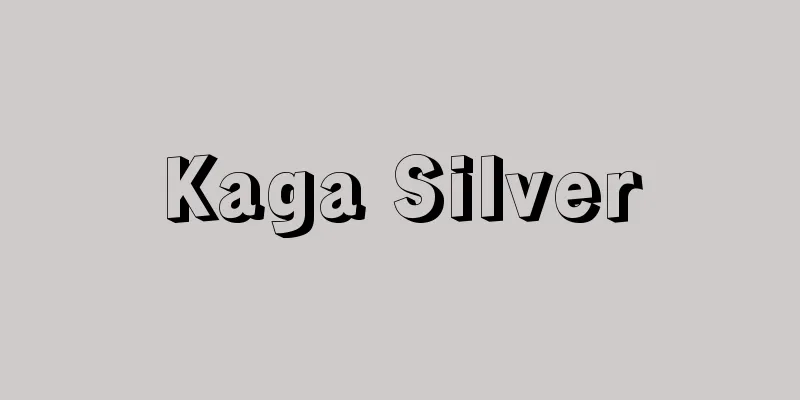

![Izuhara [town] - Izuhara](/upload/images/67caee2dbe151.webp)

![Joban Yumoto [Hot Spring] - Joban Yumoto](/upload/images/67cbdfa2f2c56.webp)


