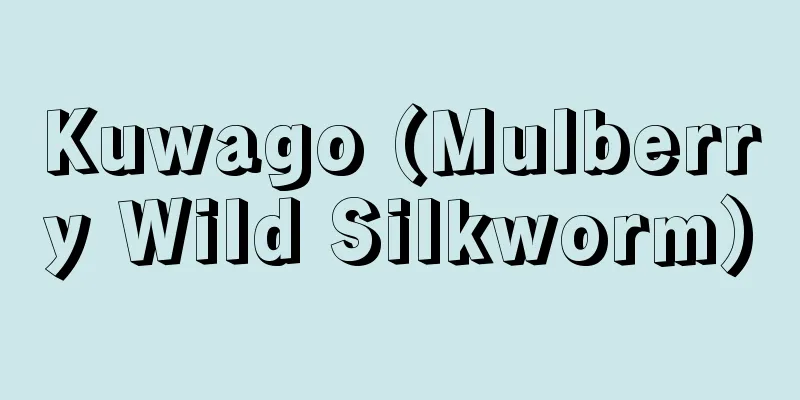Einstein's equation of specific heat

Japanese: アインシュタインの比熱式（英語表記）Einstein's equation of specific heat

This is the specific heat equation derived by Einstein to explain why the molar specific heat of a solid element is a value significantly smaller than the 3 R indicated by Dulong-Petit's law*. The lattice vibration of a crystal consisting of N atoms of the same type is considered to be a set of N independent three-dimensional harmonic oscillators that all have a common vibration frequency ν (i.e. Einstein's model*). If we consider this system of harmonic oscillators to be undergoing thermal vibration at temperature T , and use statistical mechanics to find the average value of its energy, we get

Differentiating this with respect to temperature T gives

Here, fE ( x ) = x2e /( ex ^- 1) ² is ^a function called the Einstein function. _This equation was originally devised to explain the anomaly in ^specific heat in the low temperature region, but the discrepancy becomes larger at even lower temperatures, and this difficulty was later addressed by Debye, who created a new specific heat equation. See also the entry on Debye's specific heat equation*.

Source: Asakura Publishing Dictionary of Laws Information

Japanese:

固体の元素単体のモル比熱が，デュロン‐プティの法則＊で示される3R よりかなりずれて小さな値となることを説明できるように，アインシュタインが導いた比熱式．N 個の同種原子からなる結晶の格子振動を，すべて共通の振動数 ν をもつ N 個の独立した三次元調和振動子の集合（つまりアインシュタインのモデル＊）と考える．この調和振動子の系が温度 T において熱振動しているものとして，そのエネルギーの平均値を統計力学によって求めると

となる．これを温度 T で微分すると

の形になる．ここで f_E（x）＝x²e^x/（e^x－1）² はアインシュタイン関数と呼ばれる関数である．もともと低温領域における比熱の異常性を解明するために考えられた式であるが，さらに低温となると不一致が大きくなり，この難点については後にデバイが改良を加えて新しい比熱式をつくった．デバイの比熱式＊の項も参照．

出典　朝倉書店法則の辞典について　情報

<<: Einsteinium

>>: Einstein's relation