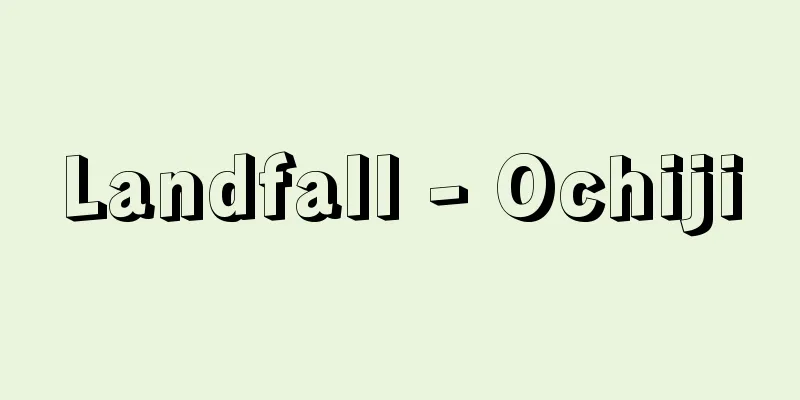Associative law

This is a law about the order of combinations of arithmetic operations. It is also called the associative law. For example, 2+(3+5) and (2+3)+5 are both equal to 10, and 2×(3×5) and (2×3)×5 are both equal to 30. For one arithmetic operation (゜) and elements a, b, and c, the combination (a゜b)゜c of a with b and the result of combining it with c is equal to the combination a゜(b゜c) of a with b and c first. In other words, this law is related only to the order of a, b, and c, and not to the order of combinations. This law not only applies to the addition (+), multiplication (×), and composition of maps (゜), but also to propositions, for example, Aand(BandC) and (AandB)andC are equivalent. However, there are many cases where the associative law does not apply, such as (2÷3)÷2＝2/6 but 2÷(3÷2)＝4/3.

[Namba Kanji]

Source: Shogakukan Encyclopedia Nipponica About Encyclopedia Nipponica Information | Legend

算法の結合の順序に関する法則。結合律ともいう。たとえば2＋(3＋5)や(2＋3)＋5はともに10であり、2×(3×5)や(2×3)×5はともに30に等しいというように、一つの算法（゜）と元a、b、cについて、最初にaとbを結合し、その結果にcを結合したもの(a゜b)゜cと、aと先にbとcを結合した結果との結合a゜(b゜c)が等しいという法則である。つまりa、b、cの順序のみに関係して結合の順には関係しないという法則である。この法則は数の加法（＋）、乗法（×）、写像の合成（゜）などについて成立するのみならず、たとえば命題についてもAand(BandC)と(AandB)andCが同値であるという意味で成立する。しかしたとえば、(2÷3)÷2＝2/6であるが2÷(3÷2)＝4/3のように結合法則の成立しない例も多い。

［難波完爾］

出典　小学館　日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について　情報 | 凡例