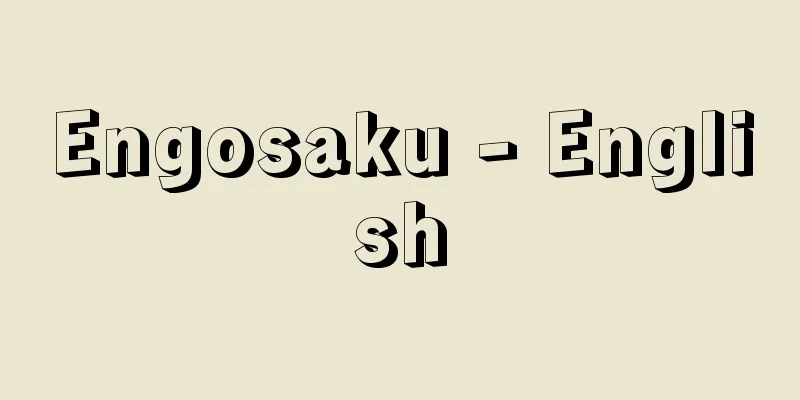Vector analysis - vector analysis

Japanese: ベクトル解析 - べくとるかいせき（英語表記）vector analysis

Vector Field

When a function f(P) = f(x,y,z) corresponds to each point P(x,y,z) in a region D of space, a scalar field f is said to be defined on D. On the other hand, when a vector-valued function F(P) = (f(P),g(P),h(P)) corresponds to D, a vector field F is said to be defined on D (or a mapping F from D to ^R3 is said to be defined). The continuity and differentiability of a vector field are defined by the continuity and differentiability of each component function.

[Haruo Sunouchi]

Gradient vector of a scalar field

For a scalar field f(x,y,z) in domain D,

A vector whose components are called the gradient vector of the scalar field f.

Alternatively, if the unit vectors in the x, y, and z directions are i, j, and k,

It can also be expressed as:

Given a scalar field f(P) with a vector field F(P),
F(P)=(gradf)(P)
When expressed as above, the vector field F is said to have a potential f, and f is called the potential of F.

[Haruo Sunouchi]

Divergence and curl of vector fields

Let F(P) = (f(P),g(P),h(P)) be the vector field defined in the domain D.

This is a scalar field, and is called the divergence of F.

is called the rotation of F. The values at these points P are expressed as (divF)(P), (rotF)(P).

Formally, a vector with differential operators as components

For a scalar field f,

For vector fields, we create the dot and cross products:

Therefore, by vector calculation,
rot(▽f)=▽×(▽f)
=(▽×▽)f=0
div(rotF) = 〈▽,▽×F〉 = 0
etc. can be obtained.

[Haruo Sunouchi]

Line integrals and Green's theorem

First, consider the two-dimensional case. Suppose a vector field F(x,y)=(f(x,y),g(x,y)) is defined for each point (x,y) in a region D on a plane. If we take a smooth closed curve C:C(t)=(x(t),y(t)) in D, the line integral of F along C is

In particular, let C be a closed curve in D, orient it counterclockwise, and let the area enclosed by C be

(Green's theorem). Using this, we can say that the vector field F(P)=(f(x,y),g(x,y)) has a potential in D if and only if the following condition is met:

(a) For P, Q∈D, the line integral of F is determined independently of the choice of the curve connecting P and Q.

Therefore,
If F=grad,

This gives us the Fundamental Theorem of Calculus.

It can be seen that this is an extension of

[Haruo Sunouchi]

Gauss's rule

Let S be a smooth closed surface, G be its enclosed domain, and n be a unit exterior normal on S. For a continuously differentiable vector field F defined in G,

where dS is the surface integral on the surface S.

[Haruo Sunouchi]

Stokes' theorem

If the boundary of the surface shown in the figure is C, then for a vector field F defined for the points of S,

Here, t is the positive unit tangent vector on the curve C, and the right-hand side is the line integral.

As an application of Gauss's theorem, for example, if we take a closed surface S in a fluid, let ρ be the density, v(x,y,z) be the velocity, and put F=ρv, the right-hand side shows that the amount flowing out of S per unit time is equal to the total amount blown out or sucked in from within G according to Gauss's theorem. Therefore, we can say that div(ρv) represents the amount of blown out or sucked in at that point.

As with Green's theorem, using Stokes' theorem, a necessary and sufficient condition for a vector field F to have potential is rotF=0. When this condition is satisfied, the product line segment of F from P to Q is independent of the curve connecting P and Q. If F=grad, then

These theorems also hold in general n-dimensional spaces.

[Haruo Sunouchi]

[Reference] | Line integral

Vector analysis (Stokes' theorem) [Diagram]
©Shogakukan ">

Vector analysis (Stokes' theorem) [Diagram]

Source: Shogakukan Encyclopedia Nipponica About Encyclopedia Nipponica Information | Legend

Japanese:

ベクトル場

空間の領域Dの各点P(x,y,z)に対し、関数f(P)=f(x,y,z)が対応するとき、D上のスカラー場fが定義されたという。これに対し、ベクトルの値をとる関数F(P)=(f(P),g(P),h(P))が対応するとき、D上のベクトル場Fが定義されたという（あるいは、DからR³への写像Fが定義されたという）。ベクトル場の連続性、微分可能性は、各成分関数の連続性、微分可能性で定義する。

［洲之内治男］

スカラー場の勾配ベクトル

領域Dにおけるスカラー場f(x,y,z)に対し、

を成分とするベクトルをスカラー場fの勾配ベクトル(こうばいべくとる)といい

で表す。あるいは、x、y、z方向の単位ベクトルをi、j、kとすると、

と表すこともできる。

　ベクトル場F(P)があるスカラー場f(P)により、
　　F(P)=(gradf)(P)
と表されるとき、ベクトル場Fはポテンシャルfをもつといい、fをFのポテンシャルという。

［洲之内治男］

ベクトル場の発散と回転

領域Dで定義されたベクトル場をF(P)=(f(P),g(P),h(P))とするとき、

をつくると、これはスカラー場で、これをFの発散という。また、

をFの回転という。これらの点Pにおける値を(divF)(P),(rotF)(P)のように表す。

　形式的に、成分として微分作用素をもつベクトル

を考え、スカラー場fに対しては

ベクトル場に対しては、内積と外積をつくると、

となる。したがってベクトル計算より、
　　rot(▽f)=▽×(▽f)
　　　　　　　=(▽×▽)f=0
　　div(rotF)=〈▽,▽×F〉=0
などが得られる。

［洲之内治男］

線積分とグリーンの定理

まず二次元の場合を考える。平面上の領域Dの各点(x,y)にベクトル場F(x,y)=(f(x,y),g(x,y))が定義されているとする。D内の滑らかな閉曲線C:C(t)=(x(t),y(t))をとると、Cに沿ってのFの線積分は、

で定義されたが、とくに、CをD内の閉曲線とし、時計と反対回りに向きをつけ、Cの囲む領域をとすると

となる（グリーンの定理）。これを用いると、ベクトル場F(P)=(f(x,y),g(x,y))がD内でポテンシャルをもつことと、次の条件とが同値であることがいえる。

（イ）　P,Q∈Dに対し、Fの線積分はP、Qを結ぶ曲線のとり方に無関係に決まる、

であるということがいえる。よって、
　　F=grad　ならば

となり、微分積分学の基本定理

の拡張になっていることがわかる。

［洲之内治男］

ガウスの定理

Sは滑らかな閉曲面、その囲む領域をGとし、nをS上の単位外法線とする。Gで定義された連続微分可能なベクトル場Fに対し、

が成り立つ。ここのdSは曲面S上の面積分である。

［洲之内治男］

ストークスの定理

図のような曲面の境界線をCとすると、Sの点に対し定義されたベクトル場Fに対し、

ここにtは曲線C上の、正の向きをもった単位接線ベクトルであり、右辺は線積分である。

　ガウスの定理の応用として、たとえば、流体の中に、閉曲面Sをとり、ρを密度、v(x,y,z)を速度とし、F=ρvと置くと、右辺がSから単位時間に流出する量、それがガウスの定理よりG内から吹き出したり、吸い込まれたりした総量に等しいことを示している。よって、div(ρv)がその点の吹き出しや吸い込みの量を表しているといえる。

　前のグリーンの定理と同様に、ストークスの定理を用いると、ベクトル場Fがポテンシャルをもつ必要十分条件は、rotF=0であり、この条件を満足するとき、FのPからQまでの積線分はP、Qを結ぶ曲線に無関係で、F=gradとすると、

　これらの定理は、一般のn次元空間でも成立する。

［洲之内治男］

[参照項目] | 線積分

ベクトル解析（ストークスの定理）〔図〕

出典　小学館　日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について　情報 | 凡例

<<: Vector space - bekutorukuukan (English spelling) vector space

>>: Vector - bekutoru (English spelling) vector