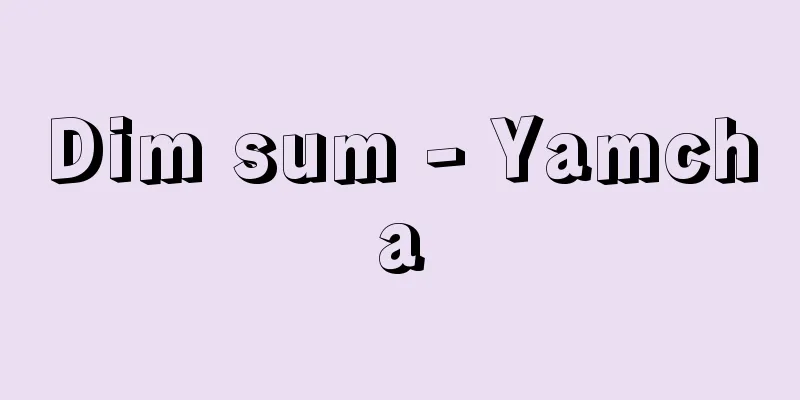Spherical trigonometry

A calculation method that uses trigonometric functions to solve problems on a sphere. It is used on Earth for surveying and navigation, and on the celestial sphere for astronomy. When a sphere is cut with a plane that passes through its center O, the curved line that is created on the sphere is called a great circle, and a figure enclosed by the minor arcs of three great circles (the shorter arcs when a great circle is divided in two) is called a spherical triangle ( Figure (1)). The points where these great circles intersect are called vertices (in this case there are three, called A, B, and C), and the arcs connecting the vertices are called sides. The angle a between the half-lines OB and OC that connect the center O and the vertices A, B, and C is directly proportional to the length of the side BC, so a can be considered a quantity that represents the length of the side. Similarly, determine angles b and c. The vertex angle A is determined as the angle between the tangents to the arcs AB and AC at vertex A. This is the same as the angle between the planes OAB and OAC ( Figure (2)). Similarly, determine vertex angles B and C. Now, E=A+B+C-π
Then, E>0 is always true. E is called the spherical excess, and the area of ​​the spherical triangle ABC is proportional to the spherical excess. In other words, if the radius of the sphere is r, then r ² E is the area.

Spherical trigonometry considers the relationships between a, b, c, A, B, and C. The basic relationships include the law of sines and the law of cosines. Using these, when one side or angle of a spherical triangle is known, it is possible to determine the other sides and angles. Spherical trigonometry developed out of necessity for navigation and other purposes, and took on the form we know today in the 14th and 15th centuries.

[Osamu Takenouchi]

Source: Shogakukan Encyclopedia Nipponica About Encyclopedia Nipponica Information | Legend

球面上の問題を解決するために三角関数を用いる計算法。地球上で応用して測量術、航海術、天球上で応用して天文学に用いられる。球をその中心Oを通る平面で切ったとき、球面上にできる切り口の曲線を大円といい、三つの大円の劣弧（大円を二分割したときの短いほうの弧）で囲まれる図形を球面三角形という（図の(1)）。この大円が交わる点を頂点（この場合三つありそれぞれA、B、Cとする）、頂点と頂点を結ぶ弧を辺という。中心Oと頂点A、B、Cを結ぶ半直線OB、OCのなす角aは、辺BCの長さと正比例するから、aは辺の長さを表す量とみなせる。同様に角b、cを定める。頂角Aは頂点Aにおける弧AB、ACへの接線の間の角として定められる。これは平面OAB、OACのなす角といっても同じことである（図の(2)）。同様に頂角B、Cを定める。いま
　　E=A+B+C-π
と置くと、つねにE＞0である。Eを球面過剰というが、球面三角形ABCの面積は球面過剰に比例する。つまり、球の半径をrとするとき、r²Eが面積である。

　このa、b、c、A、B、Cの間の関係を考えるのが球面三角法である。基本の関係として正弦法則、余弦法則がある。これらを用いて、球面三角形の辺、角の一部分がわかっているときに、他の辺、角を求めることができる。球面三角法は、航海などにおける必要から発達し、14、15世紀には今日に近い形ができあがった。

［竹之内脩］

出典　小学館　日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について　情報 | 凡例