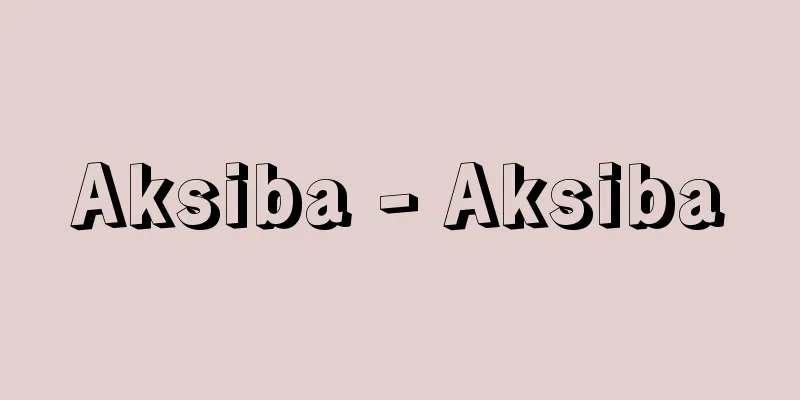Mean Value Theorem

Japanese: 平均値の定理 - へいきんちのていり

This theorem states that when a function f ( x ) is differentiable between a and b , there is at least one point between a and b that has a tangent that is parallel to the line segment connecting the points corresponding to x = a and x = b on a graph ( Figure A ). This is an important theorem that serves as the basis for deriving various theorems in differential and integral calculus. For example, the following two corollaries can be derived from the mean value theorem: [1] If f '( x ) = 0 at all times in a certain interval, then f ( x ) is a constant in this interval. [2] If f '( x ) is always ≥ 0 at all times in a certain interval, then f ( x ) is monotonically increasing in this interval.

The precise definition of the mean value theorem is as follows: If a function f ( x ) is continuous for a ≦ x ≦ b and differentiable for a ＜ x ＜ b , then it is true that a ＜ c ＜ b ,

There exists a value c such that: Note that the following variations of this are all also mean value theorems.

[Osamu Takenouchi]

Rolle's theorem

To prove the mean value theorem, one usually first deals with the special case of f ( a ) = f ( b ). When f ( a ) = f ( b ), it is called Rolle's theorem, and is stated as follows: "If a function f ( x ) is continuous for a ≦ x ≦ b , differentiable for a < x < b , and f ( a ) = f ( b ), then there exists a function c such that f '( c ) = 0 for a < c < b " ( Figure B ).

[Osamu Takenouchi]

Finite Increment Theorem

"If a function f ( x ) is continuous for a ≦ x ≦ b , differentiable for a ＜ x ＜ b , and | f '( x )| ≦ M , then
a ≦ x ＜ x ′ ≦ b , then | f ( x ′)- f ( x )| ≦ M ( x ′- x )
This is called the finite increment theorem. It follows directly from the mean value theorem, but in this form it can also be applied when f ( x ) is a vector-valued function.

[Osamu Takenouchi]

Mean value theorem for integrals

"If f ( x ) is continuous for a ≦ x ≦ b , then a ≦ c ≦ b ,

There exists a c such that

[Osamu Takenouchi]

Cauchy's Mean Value Theorem

"Let the functions f ( x ), g ( x ) be continuous for a ≦ x ≦ b , differentiable for a ＜ x ＜ b , and g '( x ) never be 0. Then,

There exists a c such that

[Osamu Takenouchi]

Mean value theorem for functions of several variables

Let us consider the case of two variables. If f ( x , y ) is partially differentiable in a neighborhood of ( a , b ), then f ( a + h , b + k )- f ( a , b ) for 0 < θ < 1.
= hf _x ( a +θ h , b +θ k )
+ kf _y ( a +θ h , b +θ k )
There exists a θ such that f _x and f _y are the partial differential coefficients.

[Osamu Takenouchi]

Mean value theorem explanation diagram (Figure A)
©Shogakukan ">

Mean value theorem explanation diagram (Figure A)

Mean value theorem (Roll's theorem) [Figure B]
©Shogakukan ">

Mean value theorem (Roll's theorem) [Figure B]

Source: Shogakukan Encyclopedia Nipponica About Encyclopedia Nipponica Information | Legend

Japanese:

関数f(x)がaとbの間で微分可能であるとき、グラフの上でx=a,x=bに対応する点を結ぶ線分に平行な接線を有する点がaとbの間に少なくとも一つあることを主張する定理（図A）。これは微分積分法における諸定理を導く基礎になる重要な定理である。たとえば、平均値の定理から次の二つの系が帰結できる。〔1〕ある区間で、つねにf′(x)=0ならば、f(x)はこの区間で定数である。〔2〕ある区間で、つねにf′(x)≧0ならば、f(x)はこの区間で単調増加である。

　平均値の定理を精密に述べると、次のようになる。関数f(x)が、a≦x≦bで連続、a＜x＜bで微分可能ならば、a＜c＜bで、

を満たすようなcが存在する。なお、この変形である以下のものも、すべて平均値の定理である。

［竹之内脩］

ロルの定理

平均値の定理を証明するためには、普通その特別な場合であるf(a)=f(b)のケースを先に扱う。f(a)=f(b)であるときをロルの定理といい、次のように表される。「関数f(x)がa≦x≦bで連続、a＜x＜bで微分可能で、f(a)=f(b)であるならば、a＜c＜bでf′(c)=0を満たすようなcが存在する」（図B）。

［竹之内脩］

有限増分の定理

「関数f(x)がa≦x≦bで連続、a＜x＜bで微分可能で、|f′(x)|≦Mであるならば、
　　a≦x＜x′≦bのとき
　　|f(x′)-f(x)|≦M(x′-x)
である」。これを有限増分の定理という。これは平均値の定理からただちに導かれるものだが、この形では、f(x)がベクトル値関数のときにも適用できる。