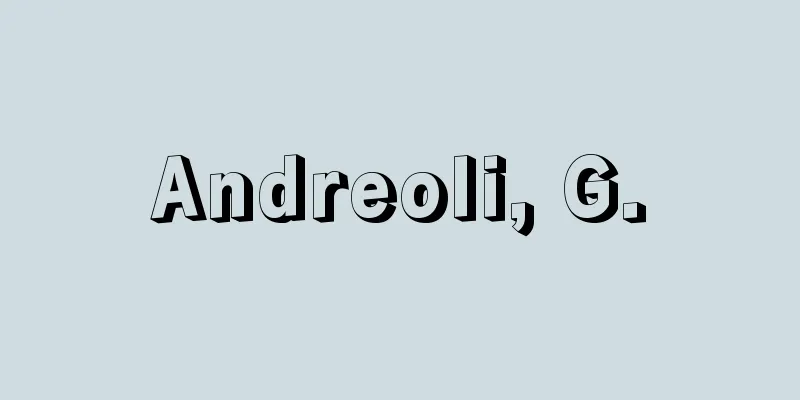Geometric sequence - Touhisuuretsu

|
A sequence of numbers created by multiplying a number by a certain number in succession. It is also called a geometric progression, and is sometimes written as GP (geometric progression). The first number is the first term, and the certain number to which it is successively multiplied is called the common ratio. If the first term is a and the common ratio is r, then the nth term, a n , is: A geometric sequence whose terms continue infinitely is called an infinite geometric sequence. This infinite geometric sequence a,ar,ar 2 ,…… [Osamu Takenouchi] Source: Shogakukan Encyclopedia Nipponica About Encyclopedia Nipponica Information | Legend |
|
一つの数に、一定の数を次々に掛けていってできる数列。幾何数列ともいい、G. P.(geometric progression)と書くこともある。最初の数を初項、次々に掛ける一定数を公比という。初項をa、公比をrとするとき、その第n項anは、 等比数列の項が無限に続くものを無限等比数列という。この無限等比数列 [竹之内脩] 出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例 |
>>: Tupi - Tupi (English spelling)
Recommend
Arbogast
…General of the late Roman Empire. A pagan Frank,...
Mount Muro - Murosan
The general term for the Muro (Obora) volcanic gro...
Shiotsuchi no Oji - Shiotsuchi no Oji
An old man who appears in Japanese mythology. He ...
Psychosurgery - Seishingeka (English spelling) psychosurgery
Psychosurgery is a brain surgery performed to res...
Yellow lily of the valley - Yellow lily of the valley
...The clustered flowers have various dark markin...
Raba porridge - Raba porridge
〘Noun〙 This refers to warm rice porridge. It is ca...
Brandenburg Concertos
A set of six concertos (BWV1046-51) composed by J...
Yoshikane Ashikaga
Year of death: 8th March 1199 (5th April 1199) Yea...
Jiraiya
Also written as Jiraiya. A phantom thief who appea...
Thermohaline circulation
...In this case, the important role is played by ...
Symplocos lucida (English spelling) Symplocoslucida
…[Yamanaka Futoshi]. … *Some of the terminology t...
Review Ceremony - Kanetsushiki
A ceremony held by the Self-Defense Forces. It is ...
chenopodium oil
...The varietal anthelminticum var. anthelminticu...
Chronological compilation of Takano's Spring and Autumn
A chronological history of Mount Koya written by t...
Fire Festival - Himatsuri
A ritual in which fire is lit to worship gods. Ma...